If it is not already apparent, by the end of this comment it should be clear why I have put these comments in this thread and not started a thread for them alone.
The Polar Science Centre has a useful page on Freeze Degree Days in the Arctic:
http://psc.apl.washington.edu/nonwp_projects/landfast_ice/freezing.phpFrom that here are the FDDs worked out for the Arctic over winter 2009 (1 September 2009 to 31 May 2010).
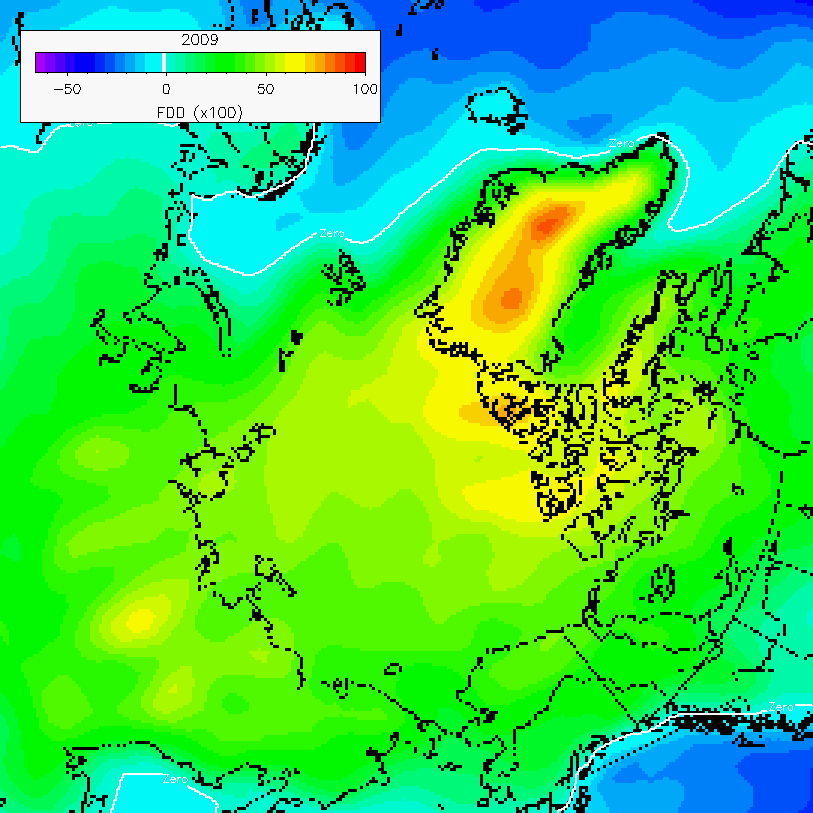
I'll be sticking to the alternate convention used in my comment above, that the winter of a particular year is from the previous September to the April of that year. But it's worth keeping in mind the sort of FDDs for 2009 and as an example the FDDs calculated for 1949 as shown below.

FDDs are very simple to work out. Freeze degree days is the sum of; the number of days below zero degC multiplied by the temperature for each day. As I have monthly average data for temperature I'll be working on a monthly basis, so for example:
December average surface temperature over the ESS in 1979 was -32.069degC, over 31 days that is 994.14 days degC (not days per degC, but days degC), calculate the FDD for each month and sum for the period September to April gives the FDD for the winter. However as I'm working off a baseline of freezing point for sea water I have added 1.8degC to get the difference between -1.8degC and the surface temperature in each month - that's what will go into an equation.
Steven was good enough to work out the equation I needed, although I already had it and was doubting it was right - that turned out to be because of a basic error in my spreadsheet. Anyway the equation was
Thickness at day n = sqrt(InitialThickness^2 + n(To-T)/804.2 )
(sqrt is 'square root', and '^' means 'to the power', i.e. InitialThickness squared.
Rewriting this in terms of FDD over September to April gives:
Thickness at day n = sqrt(InitialThickness^2 + FDD/804.2 )
Where my calculation of FDD is as explained above.
Thats the maths done with, from now on we can just think of FDDs as a handy way of combining changes in temperature and changes in freeze season length (i.e. the overall intensity of cold through the freeze season) to look at the effect on simple thermodynamic growth of sea ice.
The following graph shows April thickness from the simple model calculated as a function of each year's FDDs over winter, with September initial thickness being from the PIOMAS model.

And for comparison here is PIOMAS April thickness as a function of each year's FDDs.
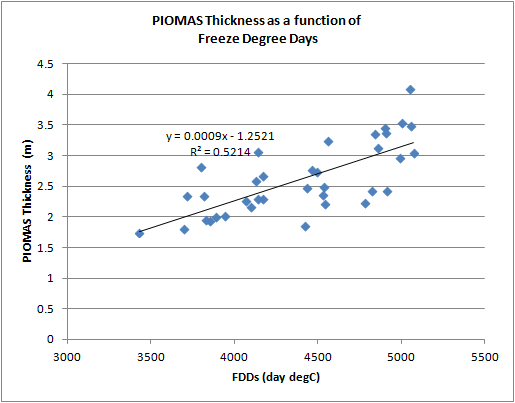
The PIOMAS relationship is weaker (R2 of 0.52) than the simple model (R2 of 0.77). As I will show below over this period the simple model is approximately linear, so without the complication of PIOMAS September thickness being used we'd probably expect that the simple model R2 for a linear line of fit should be close to 1. PIOMAS is of course a weaker fit (more scattered points) because there is a lot more going on in that model an it is closer to reality. Yes the simple model of ice growth is a bit crap, but it isn't totally useless. The scatter plot of PIOMAS and simple model April thickness shows a clear relationship, and at an R2 of 0.72 the simple model explains a significant amount of the variation in PIOMAS. PIOMAS holds a far more general form, but during winter PIOMAS thermodynamic ice growth is dominated by the simple model's physics.

If we set the simple model's initial thickness to zero then we can get a feel for how FDDs relate to April thickness in the simple model.

This graph is basically a square root plot, because taking an initial thickness of zero the equation becomes.
Thickness at day n = sqrt(FDD/804.2082)
As the 804.2082 part doesn't change it plays no role in the evolution of the graph, except by constantly scaling FDD.
But I have plotted the above with thicknesses above 1.5m highlighted by blue dots and their own trend. Down to a thickness of around 1.5m and an FDD of around 2000, April ice thickness declines linearly in relationship to FDD.
I'm interested in 1.5m as a rough figure of the sort of winter thickness that could bring about a virtually sea ice free state. I hope that those expecting a rapid transition find that this is not too conservative.
Ed Blanchard Wigglesworth gave some interesting results from PIOMAS (hat tip to Crandles), around 55 minutes into this Youtube video:
That should start where you need.
This is the graphic I'm interested in.

What the PIOMAS team did was artificially thin the sea ice by 1m in May (I think). Then the model was run using a selection of weather from recent years. The modelled ice collapses with an extraordinarily aggressive spring melt to give only remnant of thick ice off the northern coast of Canada and Greenland. In the graphic below 'control' is a set of typical PIOMAS runs for recent years (left column), 'experiment' (right column) shows what happens when the ice is thinned by 1m. Rows go from May to September.
Typical thicknesses are around 2m in recent Aprils, so somewhere between 2m and 1m thick there is potential for extremely aggressive loss of ice and virtually ice free conditions. Let's say that an April thickness of 1.5m is a reasonable compromise position for the start of the sort of losses seen in the '1m experiment'. How far away is 1.5m April thckness in terms of FDD? Well, it's an FDD of around 2000.
As shown in the graphic at the start of this comment FDDs for September to May are typically higher for a recent year like 2009. I have also calculated FDDs for the post 1979 years and plotted in the following graph.
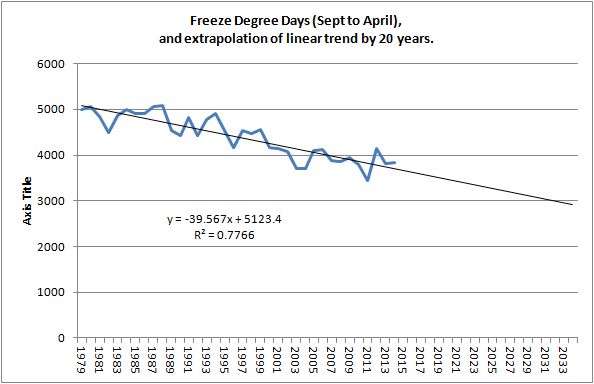
The extrapolation isn't meant to be a prediction, it's just a graphic tool to show that for FDDs to drop to around 2000 there has to be a substantial winter warming and/or a shortening of the freeze season.
Now, all of the above has been worked out using data for the East Siberian Sea (ESS), which has been seasonally ice free for some years, along with the other peripheral seas. The question has never been when will those seas beceome virtually ice free in most summers, since 2007 that has largely been the case in most years. The question is when will the Central Arctic become virtually seasonally ice free, 2012 showed that for that to happen very early melt of the peripheral seas is needed to allow substantial losses in the Central Arctic. And as the first graphic of this post shows FDD for the Central Arctic is higher than for the ESS.
Since 2001 average extent of the Central Arctic on 15 April has been 4.45M km^2. In September 2012 this had dropped to 2.81M km^2, a drop to 63% of maximum extent. To get down to 1M km^2 (August extent in the PIOMAS 1m thinning experiment) would be a drop to 22% of mid April extent.
What I hope I have shown is that the freeze season gain of thickness (hence volume) is powerful enough to keep up with summer losses, until the freeze season experiences such a combination of warming and shortening that April thickness drops to well below 2m thick. A reasonable ball park figure for expecting a virtually sea ice free state is something like 1.5m thick, but for a reduction in thermodynamic thinning to cause that 25% reduction in thickness would need a halving of current winter severity as measured by FDD.